Solving equations can feel like deciphering a secret code, and the equation 57 = -10z + 7 is no exception. It’s got all the makings of a mathematical mystery, complete with twists and turns that could leave even the most seasoned math enthusiast scratching their head. But fear not—this isn’t a high-stakes math thriller; it’s a fun journey into the realm of algebra where z is just waiting to be uncovered.
Imagine z as the elusive character in a detective novel, hiding in plain sight. With a little bit of algebraic sleuthing, anyone can crack the case wide open. So grab your magnifying glass and let’s dive into the world of numbers and operations. By the end, you’ll not only solve for z but also impress your friends with your newfound math prowess. Who knew equations could be so entertaining?
Table of Contents
ToggleOverview of the Equation
The equation 57 = -10z + 7 represents a linear equation in one variable. To find the value of z, one can manipulate the equation through algebraic operations. By isolating z on one side, it becomes easier to determine its value.
Start by moving the constant term from the right side. Subtract 7 from both sides, transforming the equation into 50 = -10z. The next step involves dividing each side by -10, which simplifies the equation further.
Calculating the division gives z = -5. This solution reveals that the variable z equates to -5, derived from systematic algebraic manipulation. Thus, the equation shows a direct relationship between constants and the variable, emphasizing clarity in mathematical reasoning.
Understanding this process encourages engagement with algebra. Anyone can identify similar patterns in other equations, reinforcing overall problem-solving skills in mathematics. Such equations underscore the importance of balancing both sides, vital to grasping more complex mathematical concepts.
Breakdown of the Equation
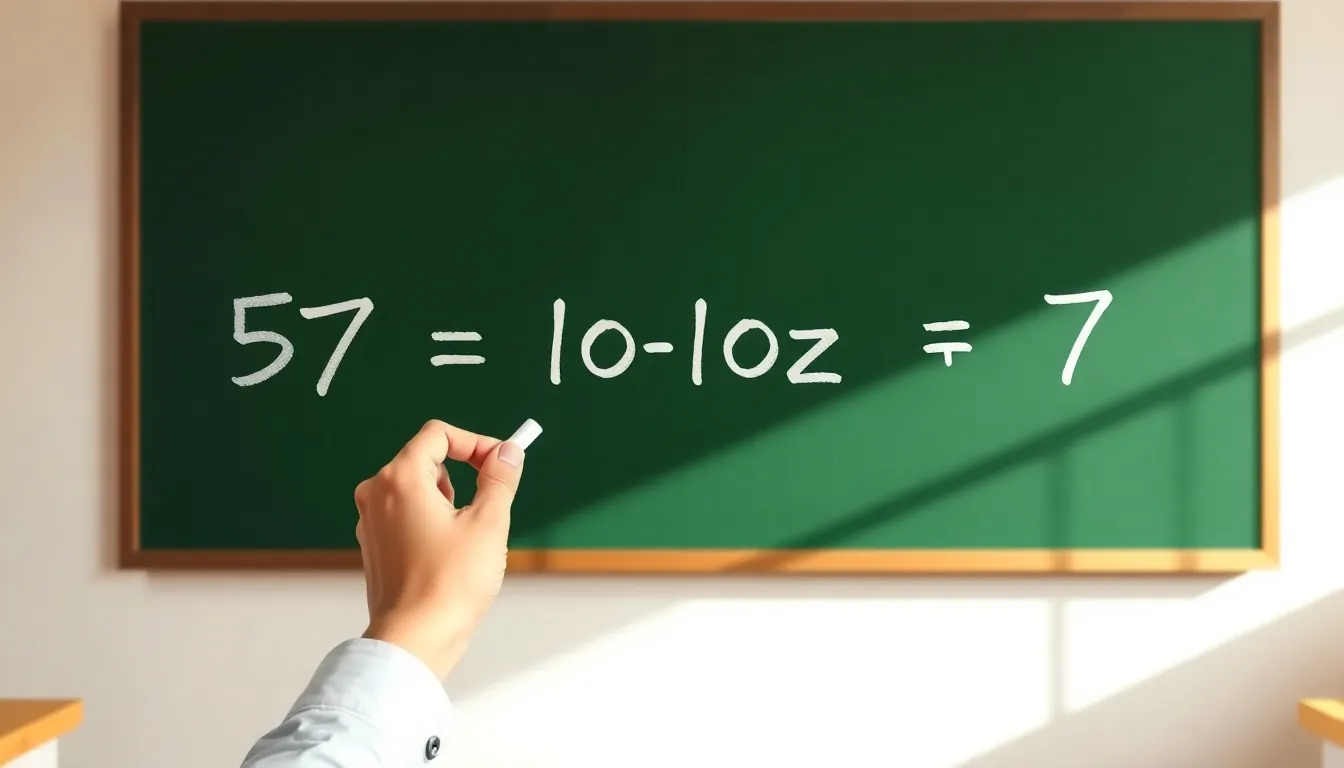
This section delves into the specifics of the equation 57 = -10z + 7, providing clarity on its components and the process to solve it.
Understanding the Variables
Variables represent unknown values in equations, and in this case, z is the key variable. The equation contains constants: 57, -10, and 7. Each constant plays a role in shaping the relationship between z and its surrounding numbers. The equation’s structure illustrates a linear relationship, where z’s value changes based on the adjustments made to the constants. Recognizing the significance of each term aids in understanding how to manipulate the equation effectively.
Isolating the Variable z
To find z’s value, start by isolating it on one side of the equation. This process begins by subtracting 7 from both sides, transforming the equation into 50 = -10z. Once the equation is simplified, divide each side by -10 to solve for z. This division leads to the conclusion that z equals -5. This method emphasizes the importance of maintaining balance in equations while systematically approaching variable isolation. Understanding these steps equips individuals with essential skills for tackling similar problems in the future.
Application of the Equation
The equation 57 = -10z + 7 finds numerous applications across various areas. Understanding its use can enhance problem-solving skills in real-world contexts.
Real-World Examples
This equation models numerous scenarios, such as budgeting and financial planning. In finance, understanding expenditures and income can reveal how adjustments impact savings. For example, if someone has $57 and spends money that can be represented by -10z, determining the appropriate adjustments helps maintain a balanced budget. Another illustration comes from physics. The equation can depict interactions between forces or energy states, simplifying complex physical phenomena into manageable calculations.
Implications in Different Fields
Different fields utilize this equation to analyze and solve problems efficiently. In economics, linear equations depict demand and supply characteristics, aiding in market analysis. Engineering also employs similar equations to optimize designs and materials, predicting outcomes based on variable changes. Environmental science uses mathematical models to study ecosystems, helping to predict outcomes under various conditions. Recognizing the significance of linear relationships provides valuable insights across disciplines and fosters critical thinking in learners.
Common Mistakes in Solving
Many students make errors when tackling the equation 57 = -10z + 7. One prevalent mistake involves failing to isolate the variable properly. Often, they forget to subtract 7 from both sides, which results in an inaccurate transformation of the equation.
Another frequent error stems from incorrect arithmetic. When students divide each side of the equation, they sometimes overlook the negative sign associated with the coefficient of z. Misinterpreting -10 as a positive value leads to an incorrect solution for z.
Confusion may also arise from misreading the equation itself. Some might attribute the wrong values to 57, -10, or 7, creating foundational inaccuracies. Recognizing each term’s role is essential for correct calculations.
Skipping steps in the solution process often leads to mistakes. To solve effectively, meticulous attention to detail is critical. Each algebraic operation should follow a logical progression to maintain clarity.
Finally, misunderstandings about linear equations can hinder progress. A lack of familiarity with the relationship between constants and variables results in careless errors. Gaining confidence in manipulating equations assists in minimizing these issues.
Addressing these common pitfalls helps learners strengthen their problem-solving skills in mathematics. By remaining attentive to each step and understanding the structure of the equation, students can successfully navigate similar problems in the future.
Solving the equation 57 = -10z + 7 not only reveals the value of z but also empowers individuals with essential mathematical skills. By engaging with the process of isolating the variable and understanding the equation’s structure, learners can build confidence in their abilities.
Recognizing the significance of each term enhances problem-solving skills and fosters a deeper appreciation for algebra. The practical applications of linear equations in various fields further illustrate their importance in everyday life.
With practice and a clear understanding of common pitfalls, anyone can navigate similar mathematical challenges with ease. Embracing these concepts lays the foundation for future success in mathematics and beyond.



